感知机算法

一、形式化定义

在机器学习中，感知机是一种用于处理监督学习的二分类问题的分类器，它是一种线性分类器，即一种基于线性预测函数（将一组权重与特征向量相结合）进行预测的分类算法，该模型有着如下的假设：

$\begin{aligned} &①处理的问题是二分类问题：e.g.~~y_i\in\{-1,+1\}\\ &②数据是线性可分的 \end{aligned}$

感知机模型最终所要求解的是权重向量$w$，其形式化定义如下：

$\begin{aligned} &权重向量：w=[w_1,w_2,...,w_d]^T\\ &特征向量：x=[x_1,x_2,...,x_d]^T\\ &解空间：\mathcal{H}=\{h(x)=w^Tx+b=0\} \end{aligned}$

二、感知机实现

2.1 权重向量

根据形式化定义，我们知道我们的求解目标是一个权重向量$w$，最终得到模型函数：$h(x)=w^Tx+b$
即我们求解得到$w$对应的是多维空间中的一个超平面$w^Tx+b=0$，该平面在多维空间中将数据点分为两部分
而我们最后的分类只需要根据$h(x)$的正负判断数据点在哪一侧即可。

权重向量$w$即为所要求解的超平面的法向量

2.2 偏差项

我们注意到模型函数中还有一项常数$b$，我们称之为偏差项，如果没有偏差项，$w$所定义的超平面一定经过原点。
为了便于后续处理，我们通过升维操作将偏差项$b$吸收到$w$中去：

$\begin{aligned} &目标超平面：w^Tx+b=0\\ &令x'=\left[ \begin{aligned} &x\\ &~1 \end{aligned} \right],w=\left[ \begin{aligned} &w'\\ &~b \end{aligned} \right]，则有w'^Tx'=w^Tx+b=0\\ &由此解空间变为：\mathcal{H}=\{h(x)=w^Tx=0\} \end{aligned}$

通过升维后超平面一定是经过原点的，则有：

$\begin{aligned} &设y_i\in\{-1,+1\},h(x_i)>0\leftrightarrow~y_i=+1,h(x_i)<0\leftrightarrow~y_i=-1\\ &可得：y_i\cdot h(x_i)=y_i\cdot(w^Tx_i)>0\leftrightarrow x_i分类正确 \end{aligned}$

注意我们尽量将二分类问题的标签设置为$\{-1,+1\}$，如果设置为$\{0,+1\}$则没有上述结论。

2.3 算法实现

首先我们先看感知机算法的伪码：

$m$用于记录在训练集上分类错误的次数，如果出错则$m=m+1$，同时对权重向量$w$进行调整，调整方式为$w=w+yx$，该调整方式的几何解释如下图所示：

如上图所示，图一为初始的权重向量以及其所对应的超平面，我们以一个标签为$-1$的数据点为例，该超平面错误得将该数据点分到了$+1$的一侧（即$y_i\cdot(w^Tx_i)\le0$），则要进行调整：$w=w+yx=w-x$，则得到了如图三所示的调整后的超平面。

数学解释如下，$w和b$的更新是一个梯度下降的过程，而我们用到的损失函数为：

$L(w,b)=-\sum_{x_i\in D}y_i(w^Tx_i+b)$

当分类错误时会有$~y_i\cdot(w^Tx_i+b)\le0~$，自然就会使得该损失函数变大，该函数对$w$和$b$求偏导得：

$\frac{\partial L(w,b)}{\partial w}=-\sum_{x_i\in D}y_ix_i\\ \frac{\partial L(w,b)}{\partial b}=-\sum_{x_i\in D}y_i$

由此我们得到更新过程：

$w\rightarrow w+y_ix_i\\ b\rightarrow b+y_i$

三、感知机的收敛

感知机可以说是第一个具有强大形式保证的算法。如果有数据集合是线性可分的，感知机将在有限更新次数中找到一个可以分离两类数据点的超平面，如果数据不是线性可分的，它将永远循环。

$\begin{aligned} &假设∃w^∗有:对于∀(x_i, y_i) ∈ D，y_i\cdot(x^Tw^∗) > 0\\ &对每个数据进行等比例收敛使得：对于\forall x_i\in D,||w^*||=\sqrt{\sum_{i=1}^n(w^*_i)^2}=1,||x_i||\le1\\ &对于w^*对应的超平面，令\gamma=\min_{(x_i,y_i)\in D}||x_i^Tw^*||，即离超平面最近的点对应的距离 \end{aligned}$

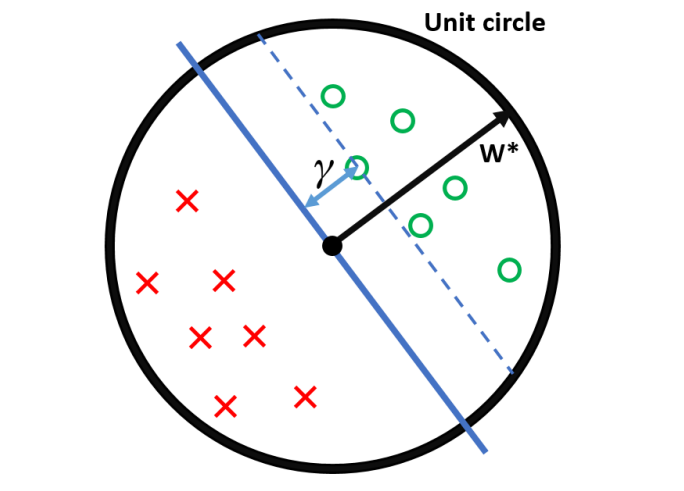
由此，我们得到一个关于更新次数和$\gamma$之间关系的定理：

定理 3-1

$感知机算法最多对超平面进行\frac1{\gamma^2}次调整$

此处的调整次数（更新次数）即为上述伪码中for循环中执行$~w=w+yx~$的次数，对上述定理的证明如下：

$\gamma$是基于上述$w^*$所对应的超平面得来的，证明过程主要讨论$w^Tw^*$和$w^Tw$的大小关系：

$\begin{aligned} 1)&如果y_i\cdot(w^Tx_i)\le0,根据算法：w=w+y_ix_i\\ &则~w^Tw^*=(w+y_ix_i)^Tw^*=(w^T+x_i^Ty_i^T)w^*=w^Tw^*+y_i\cdot(x_i^Tw^*)\\ &\because \gamma=\min_{(x_i,y_i)\in D}||x_i^Tw^*||~且~ y_i\cdot(x_i^Tw^*)>0~\therefore y_i\cdot(x_i^Tw^*)\ge \gamma\\ &\therefore w^Tw^*=w^Tw^*+y_i\cdot(x_i^Tw^*)\ge w^Tw^*+\gamma\\ 2)&如果y_i\cdot(w^Tx_i)\le0,根据算法：w=w+y_ix_i\\ &则~w^Tw=(w+y_ix_i)^T(w+y_ix_i)=w^Tw+2y_i\cdot(w^Tx_i)+y_i^2x_i^Tx_i\\ &\because y_i\in\{-1,+1\}~且~y_i\cdot(w^Tx_i)\le0,数据收敛后||x_i||_2\le1~\therefore~y_i^2=1,x_i^Tx_i\le 1\\ &\therefore~w^Tw=w^Tw+2y_i\cdot(w^Tx_i)+y_i^2x_i^Tx_i\le w^Tw+1 \end{aligned}$

调整的过程就是$w$向$w^*$趋近的过程，在算法的$for$循环中，如果进行了调整，则$w^Tw^*$至少增加了$\gamma$，$w^Tw$至多增加了1

$\begin{aligned} &设总共调整了M次，则w^Tw\le M\le\frac{w^Tw^*}{\gamma}\\ &\because ||w^*||=1~\therefore~\gamma M\le w^Tw^*\le||w^T||\cdot||w^*||=||w||=\sqrt{w^Tw}\le\sqrt{M}\\ &\therefore M\le\frac1{\gamma^2} \end{aligned}$

四、算法实现

根据上述伪码，我们将通过手动实现与调库的方式，分别实现状态机。

4.1 数据集

在本次算法实战中，我们将使用到的数据集为sklearn所提供的乳腺癌数据集，我们首先先来了解一下数据集的内容：

'''屏蔽warning'''
import warnings
warnings.filterwarnings("ignore")
'''导入重要的库'''
import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer

cancer=load_breast_cancer()
print(cancer.data)#输出数据集内容
print(cancer.target)#输出每个数据集的标签
print(cancer.feature_names)#输出数据集每一列对应的特征
print(cancer.target_names)#输出数据集的标签种类
'''将数据集存储为csv文件'''
df=pd.DataFrame(data=cancer.data,columns=cancer.feature_names)#构建二维表格
df['label']=cancer.target
df.to_csv("data/cancer_data.csv",index=False)

最终我们得到的数据集如下图所示，总共有569个数据，每条数据有30个特征，标签0，1分别代表是否患癌症。

4.2 手动实现模型

参考伪码，我们可以实现感知机的$fit$函数，在此基础上我们引入了两个新的量lr和max\text{_}iter，学习率$lr$控制每次对超平面的更新程度，最大训练轮数max\text{_}iter避免数据线性不可分时出现死循环。

'''屏蔽warning'''
import warnings
warnings.filterwarnings("ignore")
'''导入重要的库'''
import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

class Perceptron(object):
    '''初始化模型'''
    def __init__(self, learning_rate = 0.01, max_iter = 200):
        self.lr = learning_rate     #学习率
        self.max_iter = max_iter    #最大训练轮数
    '''模型训练'''
    def fit(self,data,label):                   #注意data和label都为numpy数组
        self.w = np.array([0.]*data.shape[1])   #权重向量
        self.b = np.array([0.])                 #偏差项
        iter=0                                  #训练轮数
        while True:
            m=0
            for i in range(data.shape[1]):
                x=data[i]
                y=label[i]
                if y*(np.dot(self.w,x)+self.b)<=0:#分类错误，进行更新
                    self.w=self.w+self.lr*y*x
                    self.b=self.b+self.lr*y	#注意在这里我们也对偏差项进行了更新
                    m=m+1
            if m==0:    #在训练集上没有错误
                break
            iter+=1
            if iter>=self.max_iter: #达到最大训练轮数
                break
    '''进行预测'''
    def predict(self,data):
        y_pre = np.matmul(data,self.w) + self.b
        for i in range(len(y_pre)):
            if y_pre[i]>=0:
                y_pre[i]=1
            else:
                y_pre[i]=-1
        return y_pre

'''进行预测'''
cancer=load_breast_cancer()
X=cancer.data
y=np.where(cancer.target==0,-1,1)#重点：一定要将标签修正为-1,+1
'''数据划分'''
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)#选取20%的数据作为测试集
'''初始化感知机'''
params={
    "learning_rate":0.01,
    "max_iter":250
}
perceptron=Perceptron(**params)
'''感知机训练'''
perceptron.fit(X_train,y_train)
'''模型预测与评估'''
y_pred=perceptron.predict(X_test)
print(accuracy_score(y_test,y_pred))

上述的参数得到的准确率为0.9035087719298246，我们可以通过调参过程使得准确率趋于最优。

4.3 调库实现模型

模型的训练主要用到sklearn所提供的库函数Perceptron，它的函数原型如下：

Perceptron(penalty=None, alpha=0.0001, fit_intercept=True, max_iter=None, tol=None, shuffle=True, verbose=0, eta0=1.0, n_jobs=None, random_state=0, early_stopping=False, validation_fraction=0.1, n_iter_no_change=5, class_weight=None, warm_start=False, n_iter=None)

①penalty：正则化项，$l2$、$l1$或弹性网络。
②alpha：正则化项系数，如果使用正则化项，则在正则化项前乘上该系数
③fit_intercept：是否需要计算截距
④max_iter：最大训练轮数
⑤tol：训练的停止标准，训练将在loss>previous\text{_}loss-tol时停止
⑥shuffle：是否在每轮训练后对训练数据进行随机排列
⑦eta0：学习率

'''屏蔽warning'''
import warnings
warnings.filterwarnings("ignore")
'''导入重要的库'''
import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.linear_model import Perceptron

'''进行预测'''
cancer=load_breast_cancer()
X=cancer.data
y=np.where(cancer.target==0,-1,1)#重点：一定要将标签修正为-1,+1
'''数据划分'''
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)#选取20%的数据作为测试集
'''初始化感知机'''
params={
    "penalty":"l1",
    "alpha":0.0001,
    "fit_intercept":True,
    "max_iter":200,
    "tol":0.001,
    "shuffle":True,
    "eta0":0.01
}
perceptron=Perceptron(**params)
'''感知机训练'''
perceptron.fit(X_train,y_train)
'''模型预测与评估'''
y_pred=perceptron.predict(X_test)
print(accuracy_score(y_test,y_pred))

4.4 可视化

我们不妨仅选取两个特征对模型进行训练，观察感知机模型最终得到的超平面划分是什么样的，我们利用make_classification创造具有两个特征的用于二分类的数据集，调用库函数进行预测：

'''屏蔽warning'''
import warnings
warnings.filterwarnings("ignore")
'''导入重要的库'''
import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.linear_model import Perceptron
from sklearn.datasets import make_classification

'''进行预测'''
X,y = make_classification(n_samples=1000, n_features=2,n_redundant=0,n_informative=1,n_clusters_per_class=1)
y=np.where(y==0,-1,1)
print(y)
'''数据划分'''
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)#选取20%的数据作为测试集
'''初始化感知机'''
params={
    "penalty":"l1",
    "alpha":0.0001,
    "fit_intercept":True,
    "max_iter":200,
    "tol":0.001,
    "shuffle":True,
    "eta0":0.01
}
perceptron=Perceptron(**params)
'''感知机训练'''
perceptron.fit(X_train,y_train)
'''模型预测与评估'''
y_pred=perceptron.predict(X_test)
print(accuracy_score(y_test,y_pred))
'''可视化'''
is_cancer_x,is_cancer_y=[],[]
no_cancer_x,no_cancer_y=[],[]
for i in range(len(X)):
    if(y[i]==1):
        is_cancer_x.append(X[i][0])
        is_cancer_y.append(X[i][1])
    if(y[i]==-1):
        no_cancer_x.append(X[i][0])
        no_cancer_y.append(X[i][1])
line_x = np.arange(-4,4)
line_y = line_x * (-perceptron.coef_[0][0] / perceptron.coef_[0][1]) + perceptron.intercept_
print(perceptron.coef_,perceptron.intercept_)
ax=plt.figure(figsize=(10,4),dpi=100).add_subplot()#初始化画板
ax.scatter(is_cancer_x,is_cancer_y,c="yellow",label="is_cancer")
ax.scatter(no_cancer_x,no_cancer_y,c="purple",label="no_cancer")
ax.plot(line_x,line_y,label="perceptron")
plt.legend()
plt.show()