:KNN算法.png)
机器学习实战(三):KNN算法
K-NN算法
一、形式化定义
K-NN算法(k-nearest neighbor)是一种基本的分类与回归算法,在本节我们主要以分类问题为例介绍K-NN算法。
K-NN模型是一个非参数化模型,参数数量随着训练数据的规模增长,更加的灵活,但是却又较高的计算成本。
①模型假设:相似的输入有着相似的输出
②分类规则:对于测试输入x,在其k个最相似的训练输入之间分配最常见的标签
③回归规则:输出是对象的属性值,该值是k个最近邻值的平均值。
设训练集为,输入的测试点的特征向量为,的个近邻点表示为集合,有如下性质:
根据分类规则,我们可以得到模型函数:
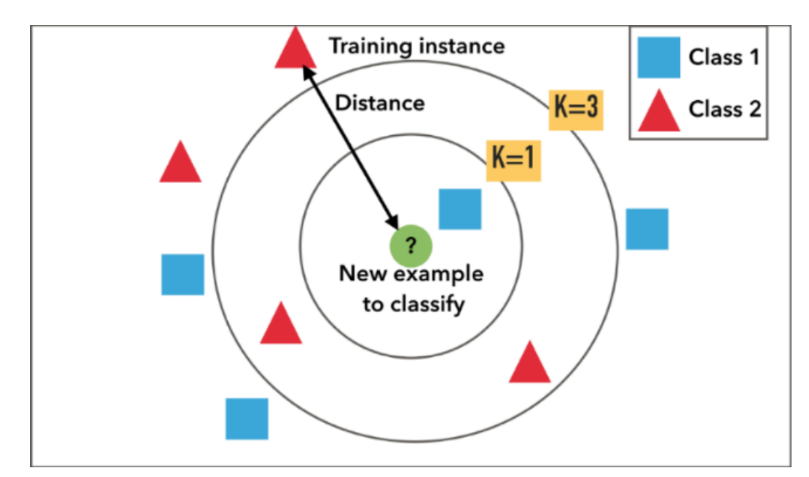
根据上述定义,我们可以通过下图更直观得认识KNN算法,当K=1时,新的数据点被分类为正方形,当K=3时,新的数据点被分为三角形
二、参数选择
2.1 距离函数
K-NN分类器基本上依赖于距离函数的选择,距离度量越能反映标签的相似性,分类器的性能就越好。
最为常用的距离函数为闵可夫斯基距离(Minkowski distance),设数据点的特征向量为维向量,则和之间的距离为:
其中,当取值不同时,得到不同的距离函数。
①时,为欧氏距离:
欧几里得度量(Euclidean Metric)是一个通常采用的距离定义,指在d维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离),在二维和三维空间中的欧氏距离就是两点之间的实际距离。
②时,为曼哈顿距离:
想象你在城市道路里,要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。
实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源,曼哈顿距离也称为城市街区距离(City Block distance)。
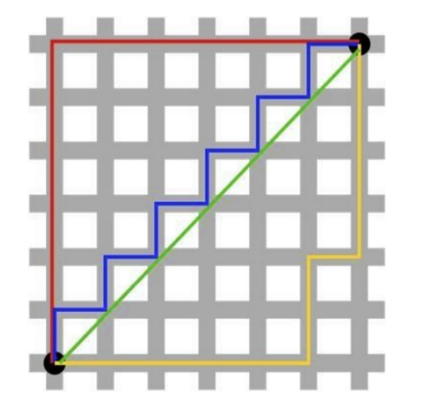
③时,为切比雪夫距离:
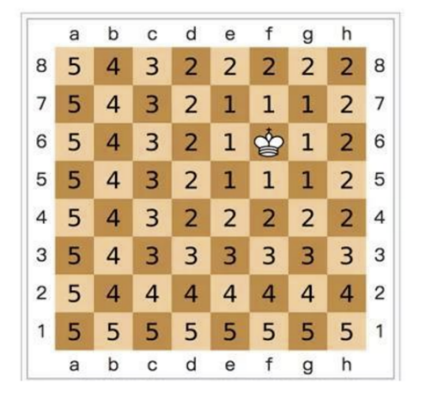
二个点之间的切比雪夫距离定义是其各坐标数值差绝对值的最大值。
国际象棋棋盘上二个位置间的切比雪夫距离是指王要从一个位子移至另一个位子需要走的步数。由于王可以往斜前或斜后方向移动一格,因此可以较有效率的到达目的的格子。上图是棋盘上所有位置距位置的切比雪夫距离。
2.2 K参数
我们应该如何选择一个合适的K值使得分类器的效果达到最优?
1)一个较小的K值:
①减少在学习过程中的近似误差,即减小在训练集上的误差
②扩大在学习过程中的估计误差,即增大在测试集上的误差
③会使得模型更加复杂,容易导致过拟合
2)一个较大的K值:
①减少在学习过程中的估计误差,即减小在测试集上的误差
②扩大在学习过程中的近似误差,即增大在训练集上的误差
③会使得模型更加简单
因此我们需要对K值进行一个权衡,这取决于所提供的数据集。通常,较大的k值会减少噪声对分类的影响,但会使类之间的边界不那么明显,在二分类问题中,选择k为奇数有助于避免并列。
三、特殊的K-NN分类器
3.1 1-NN分类器
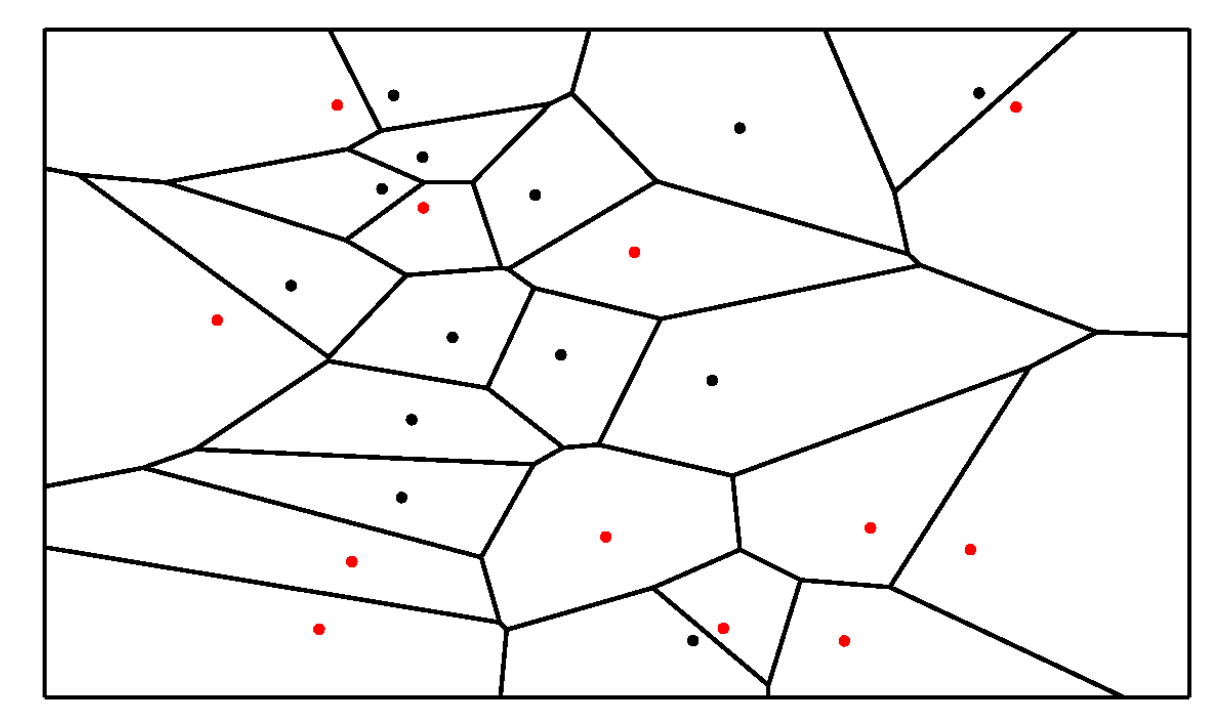
当时,我们得到的分类器便是1-NN分类器,这是一个最为直观的K-NN分类器,选取离得最近的那个数据点的标签作为预测标签。
1-NN边界划分的方法:选定每一个点最近的那个邻居,作它们连线间的中垂线,中垂线相连形成边界,得到的分类边界如下图所示
3.2 贝叶斯最优分类器
假如我们知道了任何对应的,即知道分布(这在现实中不可能),这样对于一个你就可以简单地预测最有可能的标签,Bayes optimal classifier预测为:
即:对于一个,取概率最高的标签作为预测的标签,Bayes optimal classifier 仍然可能出错,它的出错率即为:
例:假设一个二分类问题,标签仅有+1和-1两种,并且对于某个,有:
因此根据Bayes optimal classifier可得:
由此我们可以知道贝叶斯最优分类器的错误率是在给定数据分布时的最小可实现错误率。同时我们也能得到如下定理:
定理 3-1
当训练数据集的大小接近无穷大时,一个最近邻分类器(1-NN)保证错误率不低于贝叶斯错误率的两倍。
证明如下:

如上图所示,在数据集趋近于无穷大时,对于任何一个数据点,它与K个近邻的距离趋近于0,即:
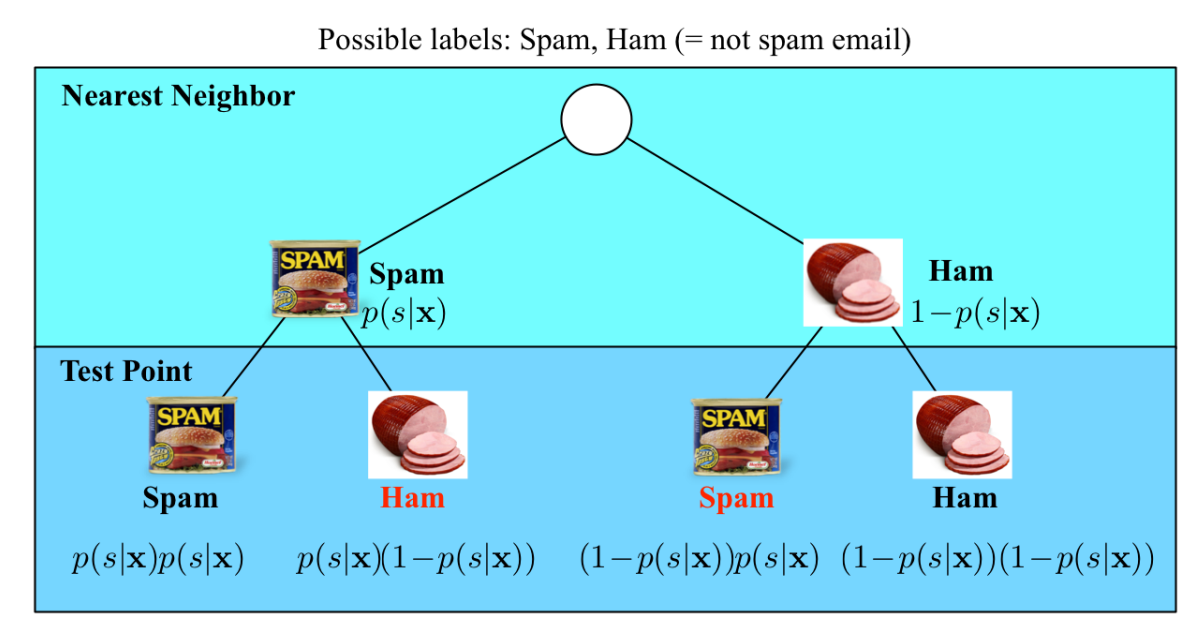
如上图所示,我们以垃圾邮件分类为例,为垃圾邮件,为正常邮件,假设的标签为,则有:
四、维度灾难
当向量的维度很高时,KNN模型将变得非常不稳定。
4.1 数据点之间的距离
首先让我们想象一个维的单位超立方体,所有的数据都在此超立方体内均匀采样,即对于任意的,都有。接着我们不妨考虑一下时,对于一个测试点它的近邻所在的超立方体,如下图所示:

设是包含个近邻的最小超立方体的边长,是取样的数据点数,因为数据集是在该单位超立方体中均匀取样,则有:
对于时的情况,则有:
| d | l |
|---|---|
| 2 | 0.1 |
| 10 | 0.63 |
| 100 | 0.955 |
| 1000 | 0.9954 |
因此,当维度很高()时,几乎需要整个空间才能找到某个测试点的10个近邻。
从而导致最近的个邻居并不比训练集中其他的点离测试点更近。
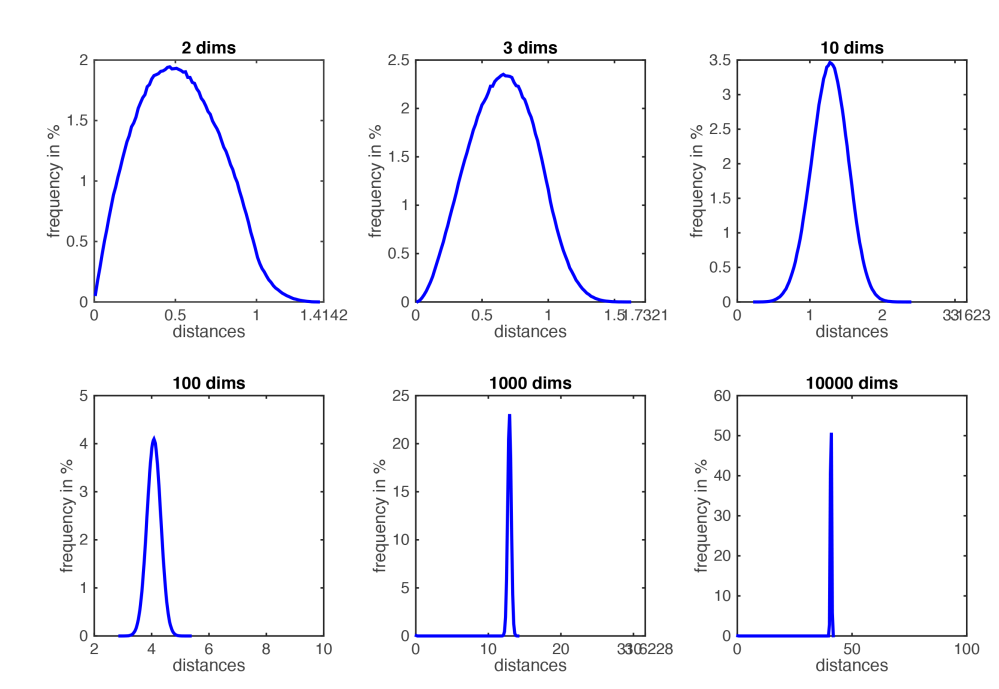
这是因为,在维空间中随机分布的点之间的距离逐渐趋近于一个很小的范围内,如下图所示:
4.2 到超平面的距离
对于二分类问题,我们往往是在维空间中寻找一个超平面,将空间一分为二,超平面两侧的数据即为不同的标签。

如上图所示,维度灾难对于两点之间的距离和点与超平面之间的距离有不同的影响。
同一维度中的移动不能增加或减少到超平面的距离,点只是四处移动并与超平面保持相同的距离。但随着维度的升高,成对点之间的距离变得非常大,到超平面的距离变得相对较小。
维数灾难的一个后果是,大多数数据点往往非常接近这些超平面,并且通常可能轻微的扰动就会更改分类。
4.3 数据降维
为了解决维度灾难,最好的方法便是对数据进行降维操作,我们以图像识别为例:虽然一张脸的图像可能需要1800万像素,但是我们可能只需要用少于50个属性(例如男性/女性、金发/深色头发等)就可以描述一个人,这些属性会随着脸的变化而变化。

如上图所示,这是从底层二维流形绘制的三维数据集示例。蓝色点位于粉色表面之上,而粉色表面则嵌入在三维空间之中,粉色表面映射为二维平面,进而将数据集从三维映射到二维,实现数据降维。
五、算法实战
本次我们使用Scikit-learn所提供的鸢尾花数据集,通过调库的方式实现K-NN算法。
5.1 数据集
我们首先了解一下该数据集的特点,读取数据并将其存储为csv文件的方式如下:
'''屏蔽warning'''
import warnings
warnings.filterwarnings("ignore")
'''导入重要库'''
import numpy as np
import pandas as pd
from sklearn import datasets
'''读取并展示数据'''
iris=datasets.load_iris()
print(iris.data)#输出数据集内容
print(iris.target)#输出每个数据集的标签
print(iris.feature_names)#输出数据集每一列对应的特征
print(iris.target_names)#输出数据集的标签种类
'''将数据集存储为csv文件'''
df=pd.DataFrame(data=iris.data,columns=iris.feature_names)#构建二维表格
df['label']=iris.target
df.to_csv("data/iris_data.csv",index=False)
我们最终得到的数据集如下图所示,总共有150个数据,每条数据有4个特征,分别为花萼长度、花萼宽度、花瓣长度、花瓣宽度,相应的不同特征所对应的标签共有3种,分别为setosa、versicolor、virginica,即鸢尾花的三个种类。

5.2 模型训练
模型的训练主要用到sklearn所提供的库函数KNeighborsClassifier,它的函数原型如下:
KNeighborsClassifier(n_neighbors=5,weights='uniform',algorithm='auto',leaf_size=30,p=2,metric='minkowski',metric_params=None,n_jobs=1,**kwargs)
①n_neighbors:即K值的大小,默认为5
②weights:用于预测的权重函数。可选参数如下:
'uniform': 统一的权重. 在每一个邻居区域里的点的权重都是一样的。
'distance' : 权重点等于他们距离的倒数。使用此函数,更近的邻居对于所预测的点的影响更大。
[callable] : 一个用户自定义的方法,此方法接收一个距离的数组,然后返回一个相同形状并且包含权重的数组。
③algorithm:计算最近邻居用的算法。可选参数如下:
'ball_tree':是为了克服kd树高纬失效而发明的,其构造过程是以质心C和半径r分割样本空间,每个节点是一个超球体。
'kd_tree':构造kd树存储数据以便对其进行快速检索的树形数据结构,kd树也就是数据结构中的二叉树。以中值切分构造的树,每个结点是一个超矩形,在维数小于20时效率高。
'brute':使用暴力搜索.也就是线性扫描,当训练集很大时,计算非常耗时
'auto':基于传入fit方法的内容,选择最合适的算法。
球树与kd树将会在后续文章中进行介绍,这是一种优化KNN算法的方式。
④leaf_size:传入BallTree或者KDTree算法的叶子数量,此参数会影响构建、查询BallTree或者KDTree的速度,以及存储BallTree或者KDTree所需要的内存大小。
⑤p:用于Minkowski metric的超参数,即当我们用闵可夫斯基距离作为度量时,p值的大小。
⑥metric:计算距离的方式,默认为闵可夫斯基距离。
我们不妨先用简单的欧几里得距离构建模型,观察模型的预测效果:
'''屏蔽warning'''
import warnings
warnings.filterwarnings("ignore")
'''导入重要库'''
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.neighbors import KNeighborsClassifier
'''模型初始化'''
params={
'n_neighbors':5,
'weights':'uniform',
'algorithm':'auto',
'leaf_size':30,
'p':2,
'metric':'minkowski',
'metric_params':None,
'n_jobs':1
}
knn=KNeighborsClassifier(**params)
'''数据集划分'''
iris=datasets.load_iris()
X=iris.data
y=iris.target
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)#选取20%的数据作为测试集
'''模型训练'''
knn.fit(X_train,y_train)
y_pred=knn.predict(X_test)
print(accuracy_score(y_test,y_pred))
在这里准确率的计算方法比较简单,即
上述模型中,我们最终在测试集上得到的准确率为0.9666666666666667,可以看出模型的效果已经非常好了。
5.3 可视化
接下来让我们进行一些调参过程,观察能否让准确率再高一些,首先调整值,对于每个值我们进行十折交叉验证:
'''屏蔽warning'''
import warnings
warnings.filterwarnings("ignore")
'''导入重要库'''
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.model_selection import KFold
from sklearn.neighbors import KNeighborsClassifier
'''模型初始化'''
params={
'n_neighbors':5,
'weights':'uniform',
'algorithm':'auto',
'leaf_size':30,
'p':2,
'metric':'minkowski',
'metric_params':None,
'n_jobs':1
}
'''数据读取'''
X=pd.read_csv("data/iris_data.csv")
y=X['label']
X.drop('label',axis=1,inplace=True)
'''创建K折交叉验证对象'''
kf = KFold(n_splits=10, shuffle=True)
'''进行交叉验证'''
K_value=[] #存储不同的K取值
Accuracy=[] #存储各个K值对应的10折交叉验证准确率
for k in range(1,31):#遍历[1,30]的K值
params['n_neighbors']=k
K_value.append(k)
acc=[]
'''对于某个K值,初始化模型'''
knn=KNeighborsClassifier(**params)
'''开始交叉验证'''
for train_index, test_index in kf.split(X):
print("TRAIN:", train_index, "TEST:", test_index)
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y.iloc[train_index], y.iloc[test_index]
'''模型训练'''
knn.fit(X_train,y_train)
y_pred=knn.predict(X_test)
acc.append(accuracy_score(y_test,y_pred))
Accuracy.append(np.array(acc).mean())
'''可视化'''
ax=plt.figure(figsize=(10,4),dpi=100).add_subplot()#初始化画板
ax.plot(K_value,Accuracy,"-.",label="score")#绘制曲线
ax.set_xlabel("K_value")#设置标签
ax.set_ylabel("Score")
plt.title("K值对准确率的影响")
'''设置中文显示'''
plt.rcParams["font.sans-serif"] = ["KaiTi"]
plt.rcParams["axes.unicode_minus"] = False
'''显示折线图'''
plt.legend()
plt.show()

如上图所示,是在在上取不同值时十折交叉验证的准确率,因为是随机对数据集进行划分,所以每次所得的曲线图是不同的,不过其大致趋势是相同的,我们最终可以得到取到能得到最高准确率的概率最高。
而其他参数的调参过程完全可以效仿上述K值调参可视化的过程,只需要修改需要遍历的取值范围以及参数名即可,即这部分代码:
for k in range(1,31):#遍历[1,30]的K值
params['n_neighbors']=k
5.4 特征重要性
因为在鸢尾花数据集中仅有4个特征,所以我们在此讨论特征重要性其实是没必要的,但是对于具有很多特征的数据集我们则需要依据特征的重要性对特征进行筛选,一方面可以提高预测的准确性,另一方面可以提高模型的效率,我们不妨先观察鸢尾花数据集的4个特征对分类准确性的影响。
我们可以通过各个特征对所对应的标签分布直观得判断特征的重要性,可视化代码如下:
'''屏蔽warning'''
import warnings
warnings.filterwarnings("ignore")
'''导入重要库'''
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.neighbors import KNeighborsClassifier
'''读取数据'''
df=pd.read_csv("data/iris_data.csv")
'''选择特征对'''
fea=("petal_length","petal_width")
'''初始化存储三种鸢尾花类型坐标的列表'''
setosa_x,setosa_y=[],[]
versicolor_x,versicolor_y=[],[]
virginica_x,virginica_y=[],[]
'''遍历数据'''
for i in df.index:
if(df['label'][i]==0):#setosa
setosa_x.append(df[fea[0]][i])
setosa_y.append(df[fea[1]][i])
if(df['label'][i]==1):#versicolor
versicolor_x.append(df[fea[0]][i])
versicolor_y.append(df[fea[1]][i])
if(df['label'][i]==2):#virginica
virginica_x.append(df[fea[0]][i])
virginica_y.append(df[fea[1]][i])
'''可视化分布'''
ax=plt.figure(figsize=(10,4),dpi=100).add_subplot()#初始化画板
ax.scatter(setosa_x,setosa_y,c="blue",label="setosa")
ax.scatter(versicolor_x,versicolor_y,c="red",label="versicolor")
ax.scatter(virginica_x,virginica_y,c="green",label="virginica")
ax.set_xlabel(fea[0])#设置标签
ax.set_ylabel(fea[1])
plt.legend()
plt.show()

我们任取两个特征,观察特征对所对应的数据分布即可判断特征的重要性,如上图所示,是我们选择petal_length,petal_width两个特征可视化的结果,可以发现三种标签的分布并没有过多的交织,说明这两个特征对于分类是较为重要的。
4个特征所对应的6个特征对的标签分布如下图所示,由此我们可以大致判断特征的重要性:

六、总结
1)如果距离可以可靠得反映相异性,则KNN是一个简单高效的模型。
2)在数据集大小时,模型将变得非常精确,但是也会变得非常缓慢。
3)当数据维度时,会发生维度灾难
4)优点:①没有关于数据的假设,例如:对非线性数据非常有用
②算法简单,易于理解
③具有较高的精度,但是与更好的监督学习模型相比没有竞争力
④用途广泛,适用于分类以及回归问题
5)缺点:①具有较高的计算成本,因为算法要用到所有的训练数据
②具有较高的内存要求,需要存储几乎所有的训练数据
③对无关特征和数据规模较为敏感,存在维度灾难












:感知机算法.png)
:监督学习.png)