:监督学习.png)
机器学习实战(二):监督学习
监督学习
一、形式化定义
在监督学习的过程中,我们输入的训练数据是成对输入的,是输入实例,是其标签,整个训练数据表示为:
其中是维特征空间,是标签空间,是第个样本的特征向量,是第i个样本的标签
数据点来自一些未知的分布
最终我们希望学习出一个模型函数,对于一个新的数据点,我们有较高概率的
监督学习的标签空间决定了问题的类型,典型的标签空间如下:
| Type | Lable Space | E.g. |
|---|---|---|
| 二分类 | E.g. 垃圾邮件过滤问题. 一个邮件要么是垃圾邮件(-1)要么不是(+1) | |
| 多分类 | E.g. 人脸识别问题.一个人的身份可以是K个身份中的一个 | |
| 回归 | E.g.预测某一天的温度或者某个人的身高 |
二、损失函数
2.1 定义
什么是损失函数?顾名思义,它是一个用于评估模型对于数据集拟合的损失程度的函数,我们希望预测的效果越差,损失函数的值越大,这也为我们在搭建模型算法的过程中提供了方向:我们要尽可能得使得模型的损失函数输出最小化,以达到较好的拟合效果。
同时在优化过程中,损失函数输出的值变化也可以说明我们的在模型优化上的进展。
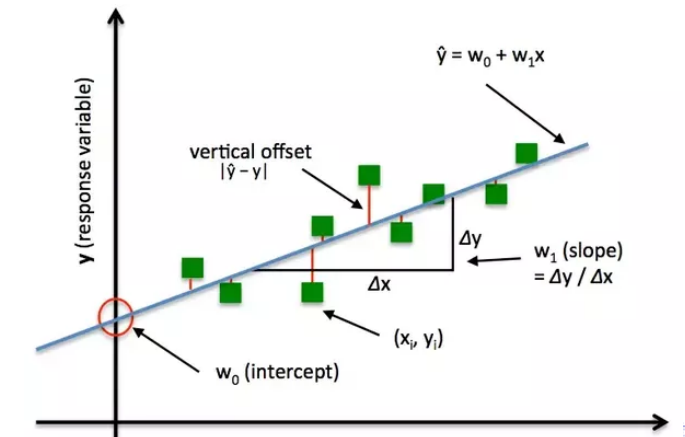
事实上,我们可以设计一个非常基本的损失函数来进一步解释它是如何工作的。对于我们所做的每个预测,我们的损失函数将简单地测量预测值和实际值之间的绝对差,即:
其中是损失函数,是我们训练出的模型函数,是验证集的样本数量,是特征向量的预测标签,则是实际的标签,显然当我们预测完全准确时,预测值与实际值差别越大,损失函数的值越大,这满足损失函数的特性。
2.2 经典的损失函数
2.2.1 Zero-one loss
0-1损失函数的形式化定义如下:
根据函数的定义,当我们的预测值准确时,会给损失函数加上0,对于不准确的预测值则会给损失函数加上1
0-1损失函数也有明显的缺点,对于分类问题影响并不大,但是对于回归问题,是某个自定义的阈值,函数对于所有的误差大于阈值的惩罚相同,即错误的预测所带来的惩罚都为1,对于一些很离谱的预测(比如1预测成了10000)并没有额外的惩罚。
2.2.2 Squared loss
平方损失函数的形式化定义如下:
平方损失函数常用于分类问题,它有两个主要特点:
①损失函数的值永远是非负的
②损失函数的值与预测的绝对误差呈二次关系
显然平方损失函数规避了0-1损失函数的缺点,对于预测误差较大的样本,所带来的惩罚也越大,但同时对于预测较准确的点,所带来的惩罚也会变得更小,对于噪声数据的处理会使得模型的效果变差。
2.2.3 Absolute loss
绝对损失函数的形式化定义如下:
绝对损失函数的值随着预测失误而线性增长,因此更适合于噪声数据
三、泛化能力
学习方法的泛化能力,是指由该学习方法学习到的模型对未知数据的预测能力,是学习方法本质上重要的性质。
对于给定的一个损失函数,我们可以得到一个使得损失函数最小化的模型,即:
机器学习的很大一部分集中在这个问题上,即如何有效地进行最小化。如果我们得到一个模型函数,它在我们的训练数据上的损失很小,我们该如何确定它在之外的数据上的损失也很小呢?这就是泛化的问题,一个泛化能力较差的模型如下:
Bad example:
对于这个模型函数,我们在训练的数据集上的误差为0,但是对于数据集外的数据点,显然将会有很大的误差,这就是过拟合问题。
四、过拟合
什么是过拟合?
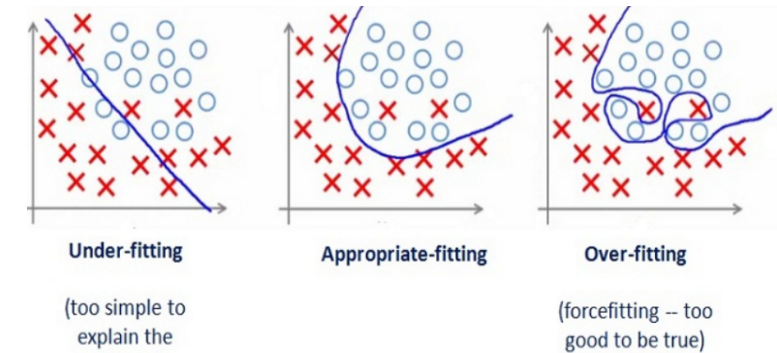
在模型的监督学习过程中,我们往往是在训练集上设计模型,在测试集上评估模型的准确性,如上图所示,图1是欠拟合的情况,即模型在训练集上也没有很好的准确性,因此在测试集上的准确性也不会高;图2是较为合适的拟合,它规避了噪声的影响,较为准确得对两类点进行了划分;图3则是过拟合的情况,它最大化了模型在训练集上的准确度而忽略了噪声点的影响,使得模型在训练集上表现得很好,但是在测试集上却表现不佳。
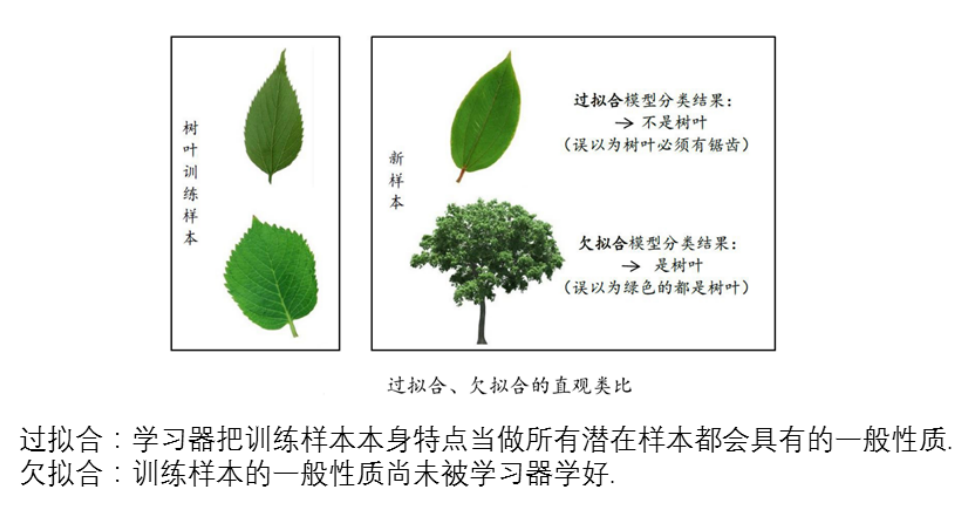
在西瓜书中也有一个比较形象的例子:
五、训练与测试
5.1 定义
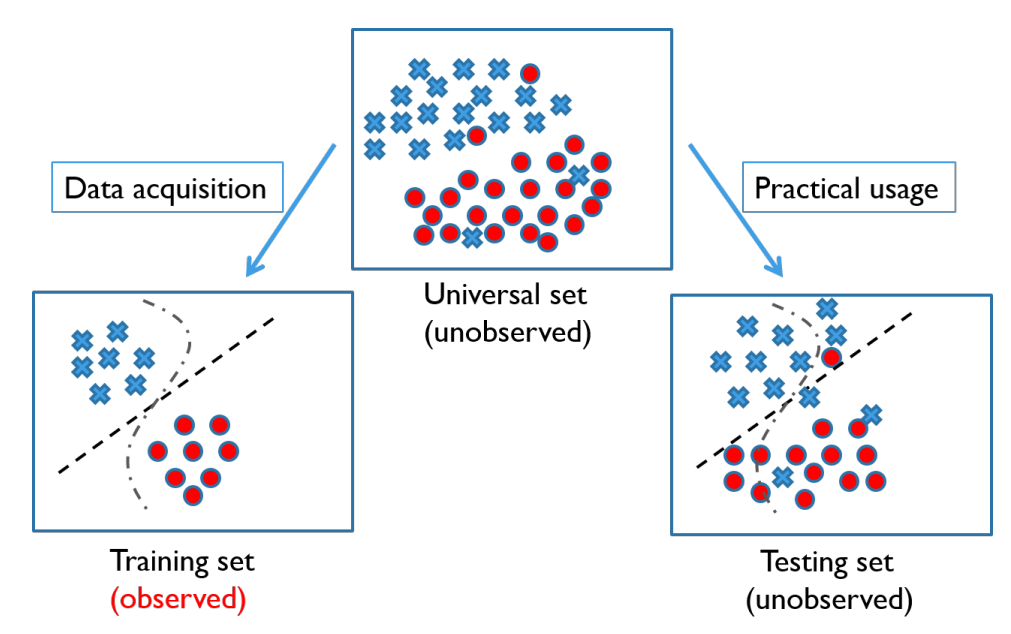
训练是使得模型可以学习的过程,而测试则是模型进行预测的过程,训练集的标签是已知的,即可观察的,而测试集的正确标签则是未知的,我们的模型要从已知的特征与标签的对应关系中进行学习,然后对未知的测试集进行预测。
**No free lunch rule:**一个模型即使在某些问题上比另一个模型好,也必然存在另一些问题使得效果比好
5.2 数据集的划分
对于所提供的数据集,为了训练模型,我们往往需要对数据集进行划分,一般划分成训练集、验证集、测试集三部分。
一般的划分比例为80%(),10%(),10%(),对于不同的数据集可以进行调整。
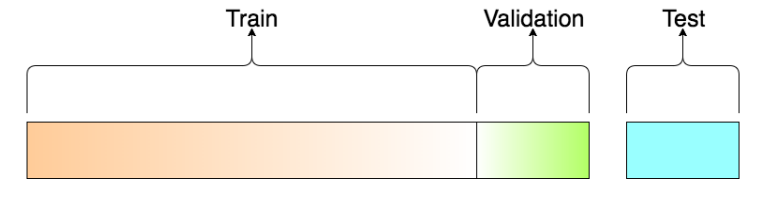
为什么我们需要验证集?
用于检查从中获得的模型函数是否存在过拟合的问题,也就是我们所追求的目标不只是在训练集上的损失最小化,也要兼顾在验证集上的损失最小化,如果在上的损失很大,将根据进行修订,并在上再次验证。该过程将不断来回,直到在上产生低损失,在验证集上的误差是接近泛化误差的。
在和的大小之间有一个权衡:对于较大的,训练结果会更好,但如果较大,验证会更可靠(噪音更少)。
对于监督学习实际的应用问题,我们一般只需要在提供的已知标签的数据集上进行训练集与验证集的划分,根据所提供的数据集的特点,有如下的划分规则:
①含有时间成分的数据集:一定要遵循过去预测未来的规则,不能利用未来的数据去预测过去的数据。
②不含有时间成分的数据集:可以均匀随机得进行划分
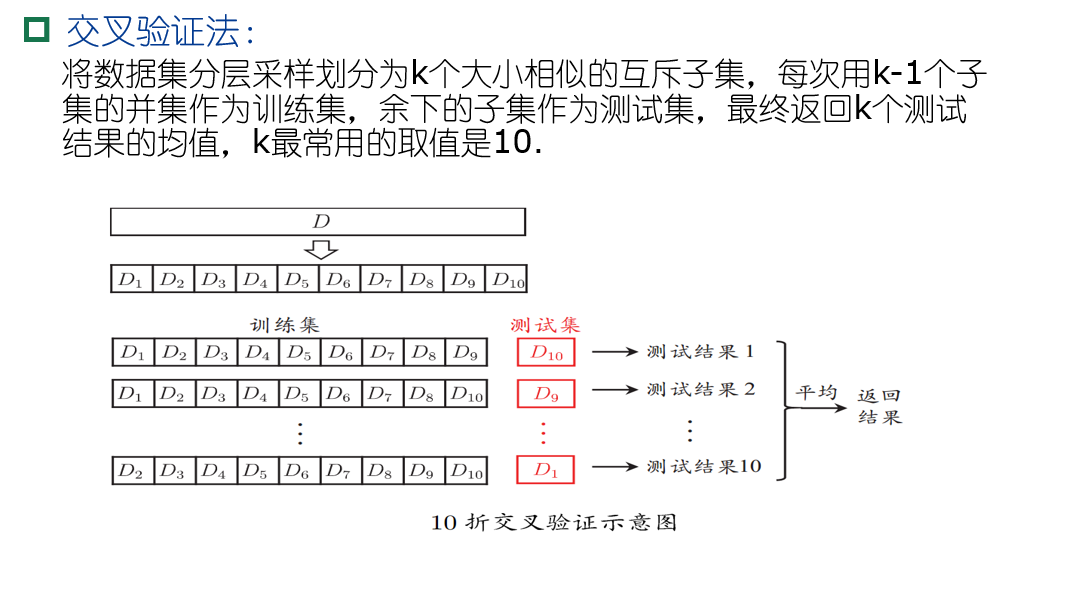
利用验证集进行模型评估的常用方法为k折交叉验证,其原理如下图所示:
六、总结
1)学习的过程:
2)评估的过程:
根据监督学习的上述基本原理,我们将在后续文章中开始相关算法的实战!












:KNN算法.png)
:机器学习导论.jpeg)